希尔排序
算法简介
希尔排序实质上是一种分组插入方法。它的基本思想是: 对于n个待排序的数列,取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列,所有距离为gap的倍数的记录放在同一个组中;然后,对各组内的元素进行直接插入排序。 这一趟排序完成之后,每一个组的元素都是有序的。然后减小gap的值,并重复执行上述的分组和排序。重复这样的操作,当gap=1时,整个数列就是有序的。
算法流程
下面以数列{80,30,60,40,20,10,50,70}为例,演示它的希尔排序过程。
第1趟: (gap=4)
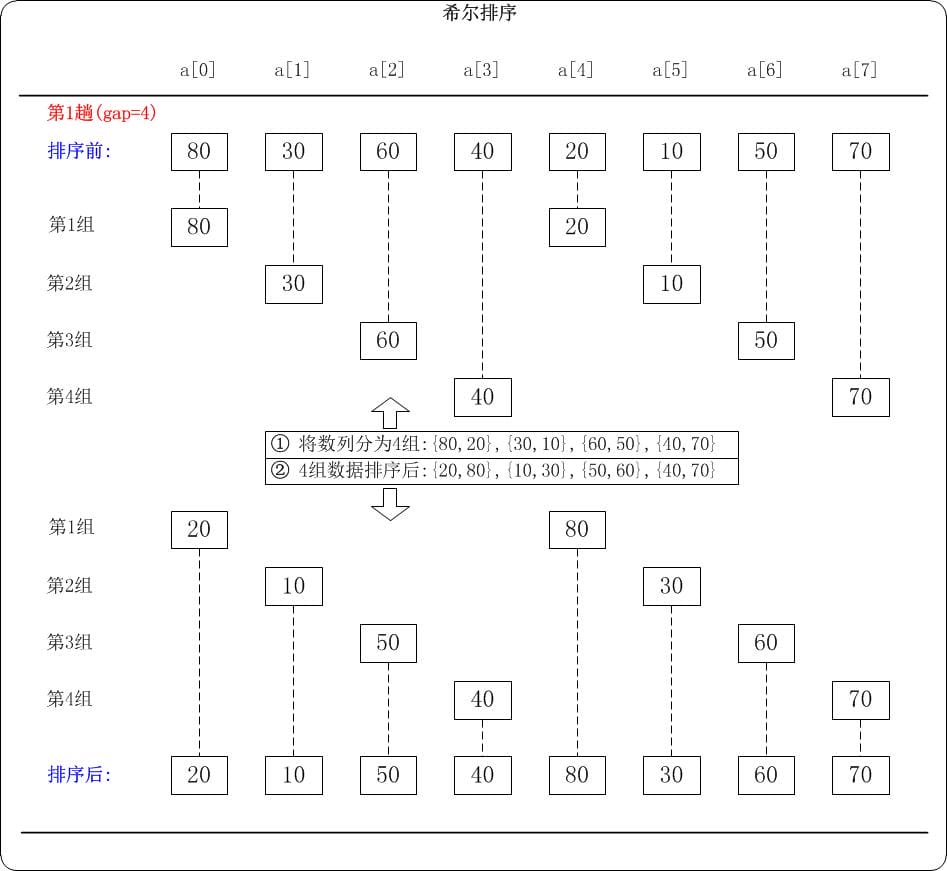
当gap=4时,意味着将数列分为4个组: {80,20},{30,10},{60,50},{40,70}。 对应数列: {80,30,60,40,20,10,50,70}
对这4个组分别进行排序,排序结果: {20,80},{10,30},{50,60},{40,70}。 对应数列: {20,10,50,40,80,30,60,70}
第2趟: (gap=2)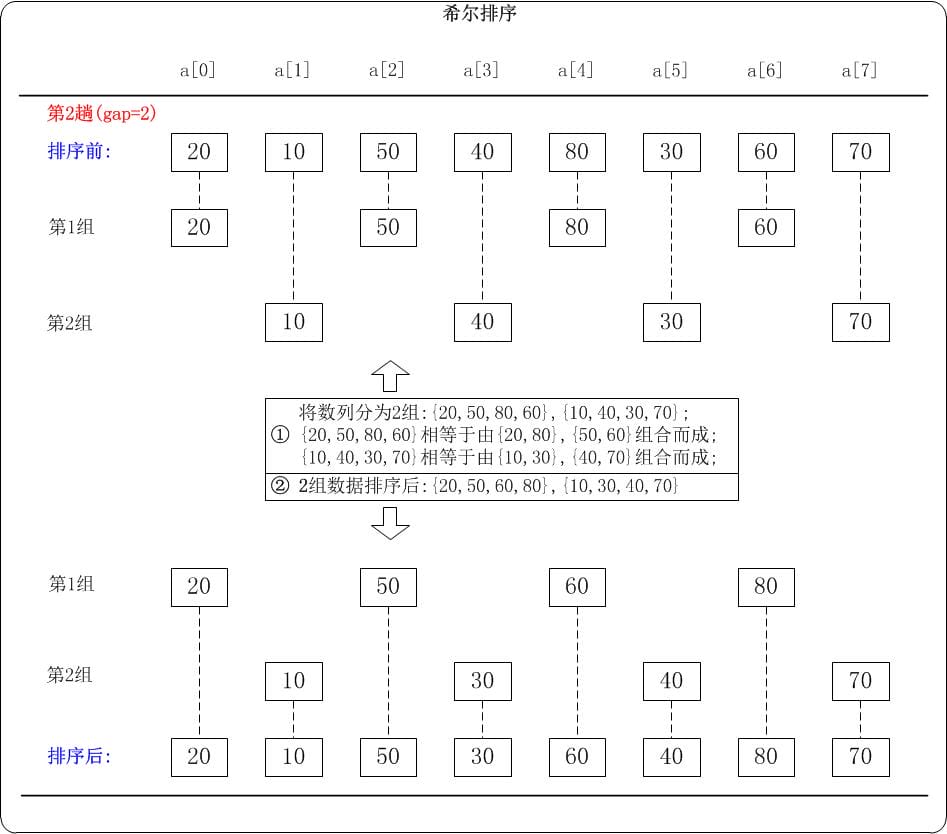
当gap=2时,意味着将数列分为2个组:{20,50,80,60}, {10,40,30,70}。 对应数列: {20,10,50,40,80,30,60,70}
注意:{20,50,80,60}实际上有两个有序的数列{20,80}和{50,60}组成。{10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。
对这2个组分别进行排序,排序结果:{20,50,60,80}, {10,30,40,70}。 对应数列: {20,10,50,30,60,40,80,70}
第3趟: (gap=1)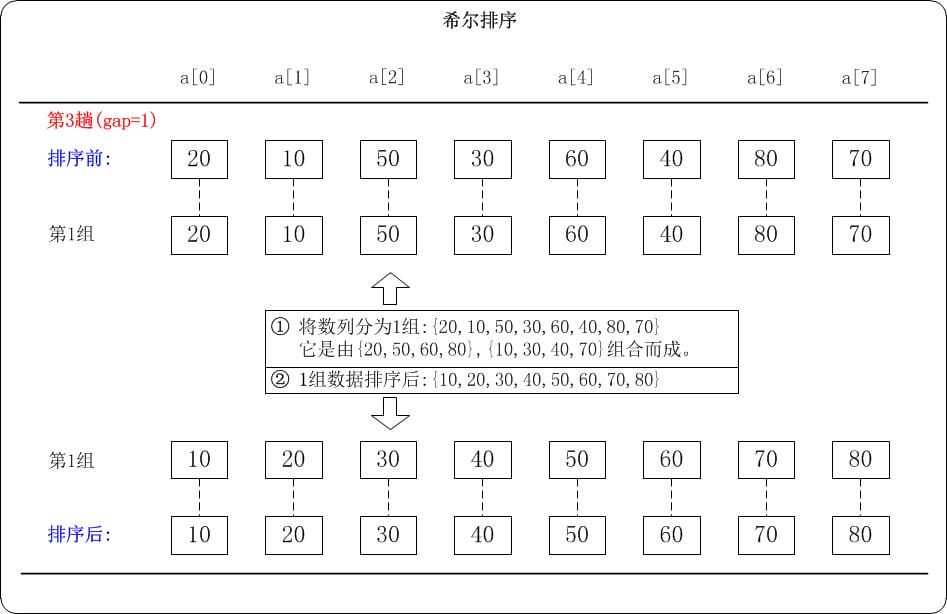
当gap=1时,意味着将数列分为1个组:{20,10,50,30,60,40,80,70}
注意:{20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。
对这1个组分别进行排序,排序结果:{10,20,30,40,50,60,70,80}
时间复杂度和稳定性
希尔排序的时间复杂度与增量(即,步长gap)的选取有关。例如,当增量为1时,希尔排序退化成了直接插入排序,此时的时间复杂度为O(N²),而Hibbard增量的希尔排序的时间复杂度为O(N3/2)。
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小, 插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
代码实现
/**
* 希尔排序: Java
*
* @author skywang
* @date 2014/03/11
*/
public class ShellSort {
/**
* 希尔排序
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
public static void shellSort1(int[] a, int n) {
// gap为步长,每次减为原来的一半。
for (int gap = n / 2; gap > 0; gap /= 2) {
// 共gap个组,对每一组都执行直接插入排序
for (int i = 0 ;i < gap; i++) {
for (int j = i + gap; j < n; j += gap) {
// 如果a[j] < a[j-gap],则寻找a[j]位置,并将后面数据的位置都后移。
if (a[j] < a[j - gap]) {
int tmp = a[j];
int k = j - gap;
while (k >= 0 && a[k] > tmp) {
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = tmp;
}
}
}
}
}
/**
* 对希尔排序中的单个组进行排序
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组总的长度
* i -- 组的起始位置
* gap -- 组的步长
*
* 组是"从i开始,将相隔gap长度的数都取出"所组成的!
*/
public static void groupSort(int[] a, int n, int i,int gap) {
for (int j = i + gap; j < n; j += gap) {
// 如果a[j] < a[j-gap],则寻找a[j]位置,并将后面数据的位置都后移。
if (a[j] < a[j - gap]) {
int tmp = a[j];
int k = j - gap;
while (k >= 0 && a[k] > tmp) {
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = tmp;
}
}
}
/**
* 希尔排序
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
public static void shellSort2(int[] a, int n) {
// gap为步长,每次减为原来的一半。
for (int gap = n / 2; gap > 0; gap /= 2) {
// 共gap个组,对每一组都执行直接插入排序
for (int i = 0 ;i < gap; i++)
groupSort(a, n, i, gap);
}
}
public static void main(String[] args) {
int i;
int a[] = {80,30,60,40,20,10,50,70};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
shellSort1(a, a.length);
//shellSort2(a, a.length);
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
参考
https://www.pdai.tech/md/algorithm/alg-sort-x-shell.html
https://www.cnblogs.com/skywang12345/p/3597597.html
