3.1 计数排序

计数排序（Counting Sort）

• 计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，快于任何比较排序算法。
• 排序思路:

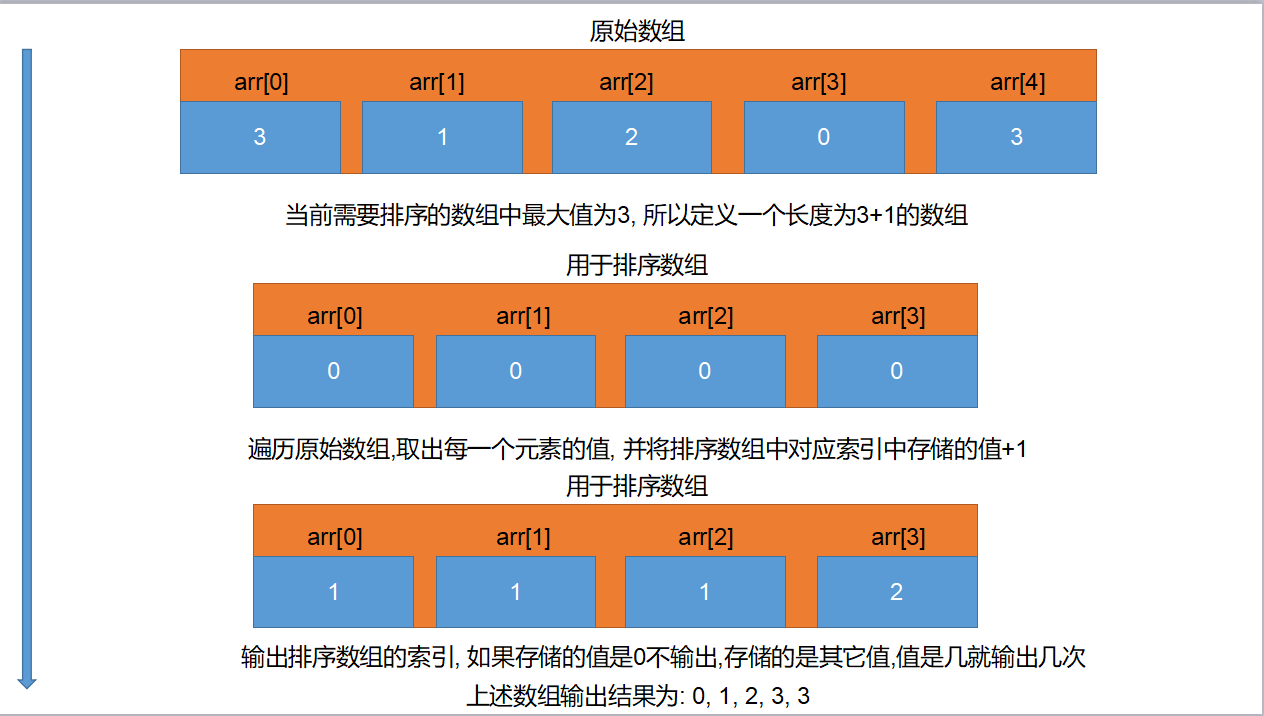
• 1.找出待排序数组最大值
• 2.定义一个索引最大值为待排序数组最大值的数组
• 3.遍历待排序数组, 将待排序数组遍历到的值作新数组索引
• 4.在新数组对应索引存储值原有基础上+1
  

• 简单代码实现:

int main()
{
    // 待排序数组
    int nums[5] = {3, 1, 2, 0, 3};
    // 用于排序数组
    int newNums[4] = {0};
    // 计算待排序数组长度
    int len = sizeof(nums) / sizeof(nums[0]);
    // 遍历待排序数组
    for(int i = 0; i < len; i++){
        // 取出待排序数组当前值
        int index = nums[i];
        // 将待排序数组当前值作为排序数组索引
        // 将用于排序数组对应索引原有值+1
        newNums[index] = newNums[index] +1;
    }
    
    // 计算待排序数组长度
    int len2 = sizeof(newNums) / sizeof(newNums[0]);
    // 输出排序数组索引, 就是排序之后结果
    for(int i = 0; i < len2; i++){
        for(int j = 0; j < newNums[i]; j++){
            printf("%i\n", i);
        }
    }
    /*
    // 计算待排序数组长度
    int len2 = sizeof(newNums) / sizeof(newNums[0]);
    // 还原排序结果到待排序数组
    for(int i = 0; i < len2; i++){
        int index = 0;
        for(int i = 0; i < len; i++){
            for(int j = 0; j < newNums[i]; j++){
                nums[index++] = i;
            }
        }
    }
    */
    return 0;
}