2.11 进制转换

进制转换

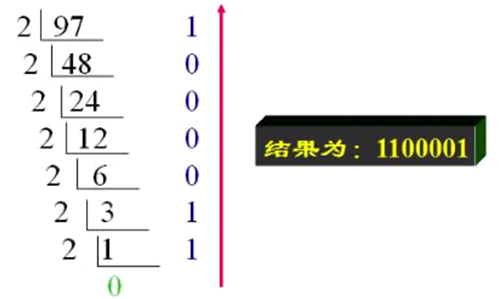
• 10 进制转 2 进制

• 除2取余, 余数倒序; 得到的序列就是二进制表示形式
• 例如: 将十进制(97) 10转换为二进制数
  

---

• 2 进制转 10 进制

  • 每一位二进制进制位的值 * 2的当前索引次幂; 再将所有位求出的值相加
  • 例如: 将二进制01100100转换为十进制

  01100100
  索引从右至左, 从零开始
  第0位: 0 * 2^0 = 0;
  第1位: 0 * 2^1 = 0;
  第2位: 1 * 2^2 = 4;
  第3位: 0 * 2^3 = 0;
  第4位: 0 * 2^4 = 0;
  第5位: 1 * 2^5 = 32;
  第6位: 1 * 2^6 = 64;
  第7位: 0 * 2^7 = 0;
  最终结果为: 0 + 0 + 4 + 0 + 0 + 32 + 64 + 0 = 100
  

---

• 2 进制转 8 进制

  • 三个二进制位代表一个八进制位, 因为3个二进制位的最大值是7，而八进制是逢8进1
  • 例如: 将二进制01100100转换为八进制数

  从右至左每3位划分为8进制的1位, 不够前面补0
  001 100 100
  第0位: 100 等于十进制 4
  第1位: 100 等于十进制 4
  第2位: 001 等于十进制 1
  最终结果: 144就是转换为8进制的值
  

---

• 2 进制转 16 进制

  • 四个二进制位代表一个十六进制位，因为4个二进制位的最大值是15，而十六进制是逢16进1
  • 例如: 将二进制01100100转换为十六进制数

  从右至左每4位划分为16进制的1位, 不够前面补0
  0110 0100
  第0位: 0100 等于十进制 4
  第1位: 0110 等于十进制 6
  最终结果: 64就是转换为16进制的值
  

---

• 其它进制转换为十进制

  • 系数 * 基数 ^ 索引 之和

      十进制           -->          十进制
     12345   =  10000 + 2000 + 300 + 40 + 5
             =  (1 * 10 ^ 4)  + (2 * 10 ^ 3) + (3 * 10 ^ 2) + (4 * 10 ^ 1) + (5 * 10 ^ 0)
             =  (1 * 10000) + (2 + 1000) + (3 * 100) + (4 * 10) + (5 * 1)
             =  10000 + 2000 + 300 + 40 + 5
             =  12345
     
     规律:
     其它进制转换为十进制的结果 = 系数 * 基数 ^ 索引 之和
     
     系数: 每一位的值就是一个系数 
     基数: 从x进制转换到十进制, 那么x就是基数
     索引: 从最低位以0开始, 递增的数
  

     二进制        -->      十进制
     543210
     101101 = (1 * 2 ^ 5) + (0 * 2 ^ 4) + (1 * 2 ^ 3) + (1 * 2 ^ 2) + (0 * 2 ^ 1) + (1 * 2 ^ 0)
            = 32 + 0 + 8 + 4 + 0 + 1
            = 45
     
     八进制        -->     十进制
     016  =   (0 * 8 ^ 2) + (1 * 8 ^ 1) + (6 * 8 ^ 0)
          =    0  + 8 + 6
          =    14
     
     十六进制      -->      十进制
     0x11f =  (1 * 16 ^ 2) + (1 * 16 ^ 1) + (15 * 16 ^ 0)
           =   256  + 16 + 15
           =   287
  

---

• 十进制快速转换为其它进制

  • 十进制除以基数取余, 倒叙读取

     十进制        -->     二进制
     100          -->    1100100
     100 / 2   = 50     0
     50  / 2   = 25     0
     25  / 2   = 12     1
     12  / 2   = 6      0
     6   / 2   = 3      0
     3   / 2   = 1      1
     1   / 2   = 0      1
     
     
     十进制        -->     八进制
     100          -->     144
     100 / 8    = 12    4
     12  / 8    = 1     4
     1   / 8    = 0     1
     
     十进制        -->     十六进制
     100          --> 64
     100 / 16   =  6    4
     6   / 16   =  0    6
  

---

十进制小数转换为二进制小数

• 整数部分,直接转换为二进制即可
• 小数部分,使用"乘2取整，顺序排列"
  • 用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,直到积中的小数部分为零，或者达到所要求的精度为止
  • 然后把取出的整数部分按顺序排列起来, 即是小数部分二进制
• 最后将整数部分的二进制和小数部分的二进制合并起来, 即是一个二进制小数
• 例如: 将12.125转换为二进制

// 整数部分(除2取余)
  12
/  2
------
   6    // 余0
/  2
------
   3    // 余0
/  2
------
   1   // 余1
/  2
------
  0   // 余1
//12 --> 1100
  
// 小数部分(乘2取整数积)
  0.125
*     2
  ------
   0.25  //0
   0.25
*     2
  ------
    0.5  //0
    0.5
*     2
  ------
    1.0  //1
    0.0
// 0.125 --> 0.001

// 12.8125 --> 1100.001

---

二进制小数转换为十进制小数

• 整数部分按照二进制转十进制即可
• 小数部分从最高位开始乘以2的负n次方, n从1开始
• 例如: 将 1100.001转换为十进制

// 整数部分(乘以2的n次方, n从0开始)
0 * 2^0 = 0
0 * 2^1 = 0
1 * 2^2 = 4
1 * 2^3 = 8
 // 1100 == 8 + 4 + 0 + 0 == 12

// 小数部分(乘以2的负n次方, n从0开始)
0 * (1/2) = 0
0 * (1/4) = 0
1 * (1/8) = 0.125
// .100 == 0 + 0 + 0.125 == 0.125

// 1100.001  --> 12.125

• 练习:
  • 将0.8125转换为二进制
  • 将0.1101转换为十进制

  0.8125
*      2
--------
   1.625  // 1
   0.625
*      2
--------
    1.25 // 1
    0.25
*      2
--------
     0.5 // 0
*      2
--------
    1.0 // 1
    0.0

// 0. 8125  --> 0.1101
1*(1/2) = 0.5
1*(1/4)=0.25
0*(1/8)=0
1*(1/16)=0.0625

//0.1101 --> 0.5 + 0.25 + 0 + 0.0625 == 0.8125